Greedy algorithms

Any algorithm that follows the problem-solving heuristic of choosing the locally best option at each stage is known as a greedy algorithm.  A greedy strategy may not produce an optimal solution in many cases, but it can produce locally optimal solutions that approximate a globally optimal solution in an acceptable amount of time.

As the name implies, a greedy algorithm always chooses the option that appears to be the best at the time. This means it will make a locally optimal decision in the hopes of arriving at a globally optimal answer.

For example, a greedy strategy for the travelling salesman problem (which has a high computing cost) is to "visit the nearest unvisited city at each step of the route. This heuristic does not aim to discover the best answer, but it does it in a fair number of steps; finding the best solution to such a difficult problem usually takes an unreasonable amount of time. Greedy methods are used in mathematical optimization to solve combinatorial problems with matroid qualities and to yield constant-factor approximations to optimization problems with the submodular structure.

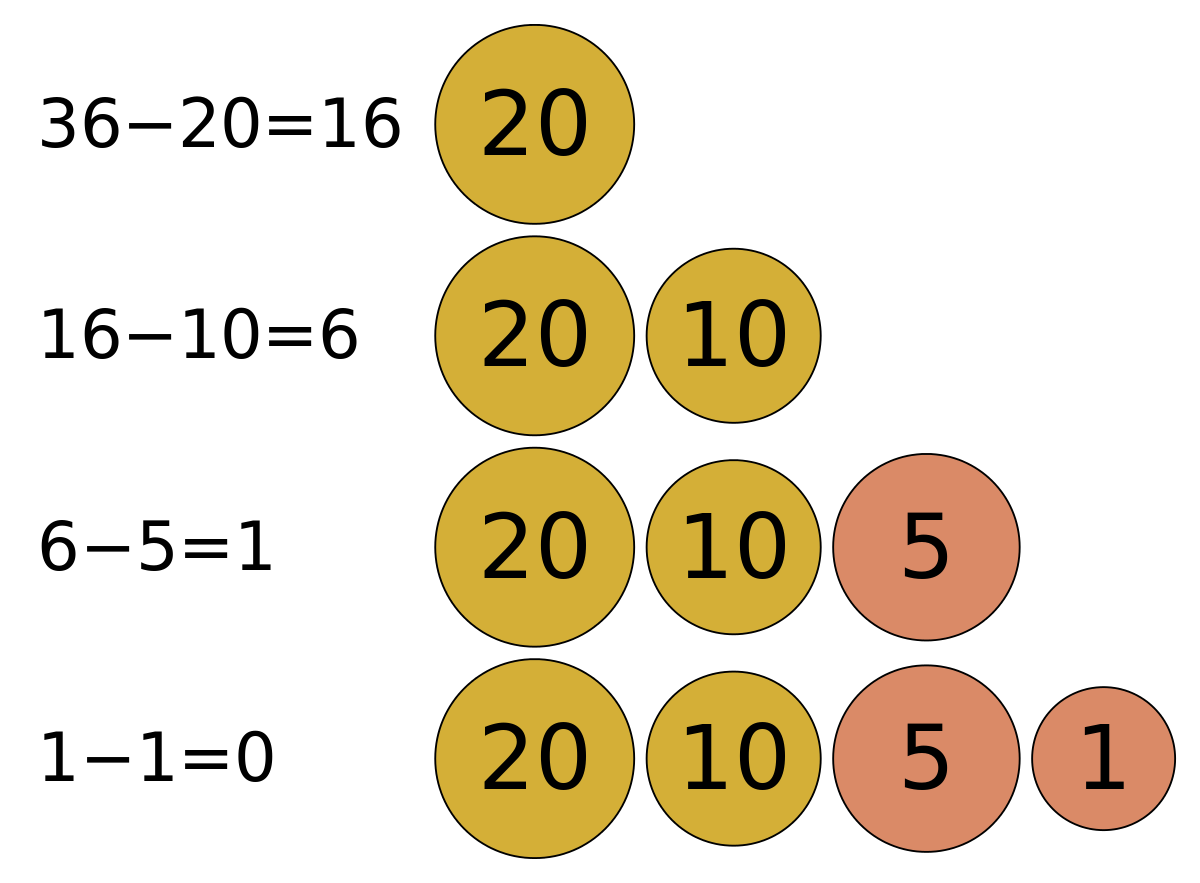
Greedy Approach

1. Let's start with node 20 (the root). The right youngster weighs 3 pounds, whereas the left child weighs 2.

2. Our goal is to discover the longest path possible. And, at the moment, the best solution is 3. As a result, the greedy algorithm will pick number three. Finally, the weight of a three-year-old lone child is 1. As a result, our final answer is 20 + 3 + 1 = 24.

It is, however, not the best option. As seen in the graphic below, there is another method that bears greater weight (20 + 2 + 10 = 32).

Greedy algorithms are classified as "short-sighted" and "non-recoverable." They're only useful for problems with a 'optimal substructure.' Despite this, the best-suited algorithms for many simple problems are greedy. It's worth noting, however, that the greedy algorithm can be employed as a branch-and-bound method or a selection algorithm to rank choices inside a search. The greedy algorithm has a few different variations:

 

·         Pure greedy algorithms

·         Orthogonal greedy algorithms

·         Relaxed greedy algorithms

Standard Greedy Algorithms:

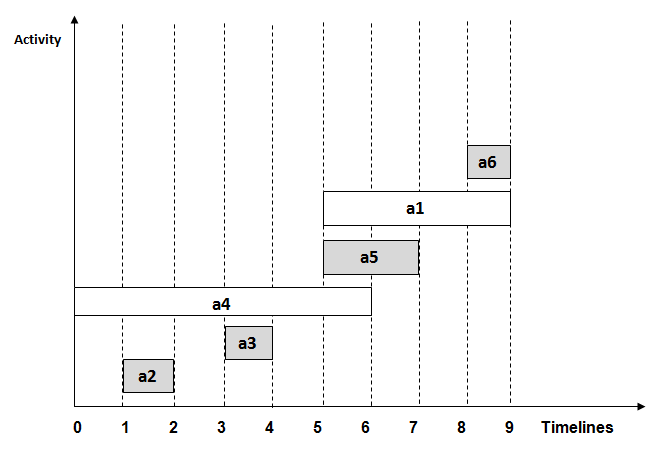
1.Activity Selection Problem

Greedy is an algorithmic paradigm that assembles a solution piece by piece, constantly opting for the next component that provides the most evident and immediate benefit. For optimization issues, greedy algorithms are used. Greedy can solve an optimization problem if it has the following property: At each stage, we can select the best choice that looks best at the time, and we receive the best solution for the entire problem.

If a Greedy Algorithm can solve a problem, it is usually the optimal approach for doing so since Greedy algorithms are more efficient than alternative techniques like Dynamic Programming. However, greedy algorithms are not always applicable. The Fractional Knapsack problem, for example, can be solved with Greedy, whereas the 0-1 Knapsack problem cannot.

The following are some examples of standard greedy algorithms.

1)   Kruskal's minimum spanning tree: We make an MST using Kruskal's algorithm by picking edges one by one. The Greedy Option is to choose the lightest weight edge that does not generate a cycle in the MST that has so far been constructed.

 2) Prim's minimum spanning algorithm: We generate an MST by picking edges one by one in Prim's algorithm as well. We keep two sets of vertices: one for those that are already in MST and another for those that aren't yet. Picking the smallest weight edge that connects the two sets is the Greedy Option.

 3) Dijkstra's Shortest Path: Dijkstra's and Prim's algorithms are quite similar. Edge by edge, the shortest-path tree is constructed. We keep two sets of vertices: one for those that have already been added to the tree, and another for those that have not yet been added. The Greedy Choice is to choose the edge that connects the two sets and is on the shortest weight path from the source to the set with vertices that have not yet been included.

 4) Huffman Coding: The Huffman Coding Method is a lossless compression method. It assigns distinct characters variable-length bit codes. The Greedy Option is to assign the character with the shortest bit length code.

For Hard optimization issues, greedy techniques are sometimes utilised to gain an approximation. The Traveling Salesman Problem, for example, is an NP-Hard problem. At each stage, a greedy solution to this problem is to choose the next unvisited city from the current city. These solutions do not necessarily yield the best ideal solution, but they can be utilised to obtain a close match.

Time Complexity: It takes O(n log n) time if input activities may not be sorted. It takes O(n) time when it is given that input activities are always sorted.

Knapsack problem 

The knapsack problem is a combinatorial optimization problem that entails: Determine the quantity of each item to include in a collection given a set of objects, each with a weight and a value, so that the total weight is less than or equal to a given limit and the total value is as large as possible. It gets its name from the issue that someone with a fixed-size knapsack faces when they have to fill it with the most precious stuff. The issue frequently arises in resource allocation, as decision makers must choose among a set of non-divisible projects or activities while working under a strict budget or time constraint.

The knapsack problem has been investigated for almost a century, with the first papers dating back to 1897. The term "knapsack problem" is derived from the early works of mathematician Tobias Dantzig (1884–1956), and relates to the challenge of packing the most expensive or helpful objects without overcrowding the luggage.

2. Job Sequencing Problem

Given a list of jobs, each with its own deadline and related profit if completed before the deadline. Given that each activity takes a single unit of time, the shortest deadline conceivable for any job is 1. When just one work can be booked at a time, how can overall profit be maximised? A simple solution is to produce all subgroups of a given set of jobs and then examine the feasibility of jobs in each subset individually. Maintain a running total of the greatest profit from all possible subgroups. This solution has an exponential temporal complexity.

This is a typical Greedy Algorithm scenario. The Time Complexity of the above solution is O(n2). It can be optimized using Priority Queue(max heap).

The algorithm goes as follow:

·         Sort the jobs based on their deadlines.

·         Iterate from the end and calculate the available slots between every two consecutive deadlines. Include the profit, deadline, and job ID of ith job in the max heap.

·         While the slots are available and there are jobs left in the max heap, include the job ID with maximum profit and deadline in the result.

·         Sort the result array based on their deadlines.

3. Greedy Algorithm for Egyptian Fraction:

Every positive fraction can be expressed as a collection of distinct unit fractions. If the numerator is 1 and the denominator is a positive integer, the fraction is called a unit fraction. For example, 1/3 is a unit fraction. Egyptian Fraction was the name given to this type of representation since it was employed by ancient Egyptians.

Using the Greedy Algorithm, we can construct Egyptian Fractions. Find the highest feasible unit fraction for a given number of the type 'nr/dr' when dr > nr, then repeat for the remaining part. Taking 6/14 as an example, we first determine a ceiling of 14/6, i.e. 3. As a result, the initial unit fraction becomes 1/3, and the process repeats for (6/14 – 1/3), or 4/42. Because a fraction is always reduced to a form where the denominator is bigger than the numerator and the numerator does not divide the denominator, the Greedy algorithm works. The highlighted recursive call for decreased numerator is made for such reduced forms. As a result, the recursive calls continue to reduce the numerator until it approaches 1.

4. Efficient Huffman Coding for Sorted Input:

The above-mentioned algorithm has an O time complexity (nLogn). We can create Huffman codes in O(n) time if we know the provided array is sorted (in non-descending order of frequency). For sorted input, here is an O(n) algorithm.

1. Begin by making two empty queues.

2. For each unique character, create a leaf node and enqueue it to the first queue in non-descending order of frequency. The second queue is initially empty.

3. Examine the front of both queues to dequeue two nodes with the lowest frequency. Repeat the procedure two more times.

1. Dequeue from first queue if second queue is empty.

2. Dequeue from second queue if first queue is empty.

3. If not, compare the fronts of two queues and dequeue the one with the shortest wait time.

4. Make a new internal node with the frequency of the two nodes added together. Make the left child of the first Dequeued node and the right child of the second Dequeued node. Add this node to the second queue.

5. If there are multiple nodes in the queues, repeat steps #3 and #4. The root node is the last node in the tree, and it completes it.

Applications

Greedy algorithms frequently (but not always) fail to identify the globally optimal solution because they do not run through all of the data exhaustively.

 They may make premature commitments to certain options, preventing them from later determining the greatest overall answer.

 For example, none of the existing greedy colouring algorithms for the graph colouring problem or any other NP-complete problem consistently provide optimal solutions.

 Nonetheless, they're useful because they're quick to come up with and frequently provide good approximations to the ideal.

If a greedy algorithm can be shown to generate the global optimum for a specific problem class, it is often chosen over alternative optimization approaches such as dynamic programming since it is faster.

Kruskal's and Prim's algorithms for finding minimum spanning trees, as well as the technique for finding optimum Huffman trees, are examples of greedy algorithms.

 

Examples

• The activity selection problem is typical of this type of problem, in which the goal is to select the greatest number of activities that do not conflict

• Crystal Quest is a Macintosh computer game in which the goal is to collect crystals in a manner similar to the travelling salesman dilemma. In the demo mode, the game uses a greedy method to visit all of the crystals. Because the artificial intelligence fails to account for obstructions, the demo mode frequently terminates prematurely.

• The signal approximation matching pursuit is an example of a greedy algorithm.

• Greedy algorithms are often employed in decision tree learning, although they are not guaranteed to find the best solution.

• For decision tree creation, one prominent approach is the ID3 algorithm.

• For graph search and shortest path finding, Dijkstra's algorithm and the related A* search algorithm are verifiably optimum greedy algorithms.

• o An "admissible heuristic" that does not overstate path costs is required for A* search to be conditionally optimal.

• • Kruskal's and Prim's algorithms are greedy methods for constructing the shortest spanning trees in a linked network. They always find the best solution, which may or may not be unique.

Conclusion

It is best applicable when one needs a solution in real-time and approximate answers are “good enough”. Clearly, it minimizes time while making sure that an optimal solution is produced; hence it is more applicable to use in a situation where less time is required. Post-reading this article, one might have a fair idea about greedy algorithms. In addition, this post explains why it is regarded as the best framework that answers nearly all programming challenges along with helping you to decide the most optimal solution at a given point in time.

However, on the rough side, for applying the theory of greedy algorithms, one must work harder to know the correct issues. Although it’s a scientific concept that has logic, it also has an essence of creativity.